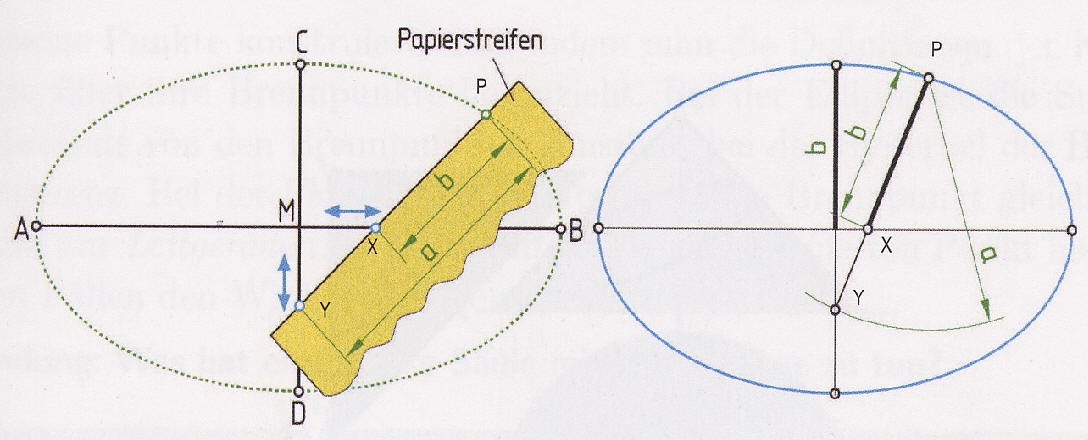
Nichtlineare Analytische geometrie der ebene:
Dazu einige hilfreiche
Bemerkungen:
- Wir werden vom 3. bis zum 18. Oktober zwölf
dieser 39 Übungsaufgaben im Unterricht behandeln, drei weitere werden
HÜ-Beispiele sein.
- In der 7A (die ich regulär - im Sinne von
nicht nur vertretungsweise! - unterrichte) werden ebenso zwölf SÜ- und drei
HÜ-Beispiele aus der gleichen Aufgabensammlung
verwendet, jedoch gänzlich andere als jene aus "eurer 15er-Gruppe".
- Somit bleiben (für euch wie auch für die 7A!)
neun der 39 Aufgaben als reine Übungsaufgaben für die 1. Schularbeit übrig.
- Wisst diesen Umstand für euch zu nutzen! D.h.
übt für die Schularbeit nicht nur anhand der neun übrigbleibenden Beispiele,
sondern auch mit Hilfe jener 15 Aufgaben, welche wir nicht (die 7A aber schon)
in SÜen oder HÜen behandelt haben, jedoch mit der Möglichkeit, sich mit der 7A
ein wenig auszutauschen (Immerhin habt ihr ja dann auch 15 Aufgaben, die in
der 7A weder in SÜen noch HÜen behandelt wurden!).
- Ein alternativer Einstieg zur analytischen Geometrie der Parabel (nebst Ellipse,
Hyperbel, Kreis, Punkt, Doppelgerade, Geradenpaar, Parallelenpaar und leerer
Menge der neunte Kegelschnittstyp!), der erst nach Kenntnis der analytischen
Geometrie der Ellipse (folgt Ende Oktober sowie den ganzen November) bei
Interesse selbst
HIER
durchgegangen werden kann, ergänzende (wertvolle, unterstützende, per se
interessante ... ☺) Informationen zur Parabel
(welche aber nicht so reichhaltig als jene für die Ellipse weiter unten sind)
findest du
hier (und kannst du schon vor der Behandlung
der Ellipse bereits Anfang Oktober wirklich sinnbringend selbst studieren!)
- Diverse Übungsaufgaben findest du weiter unten!
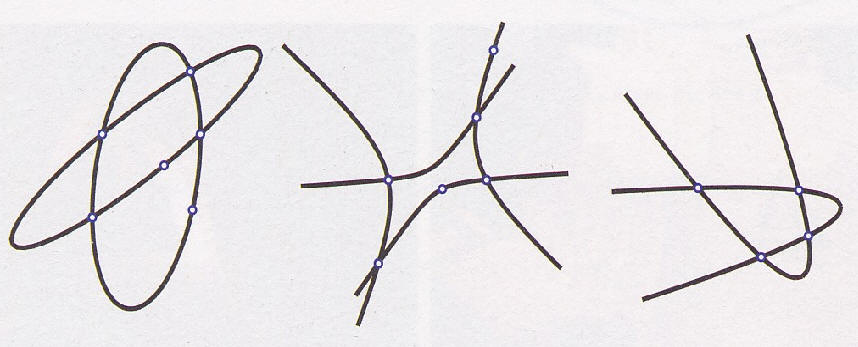
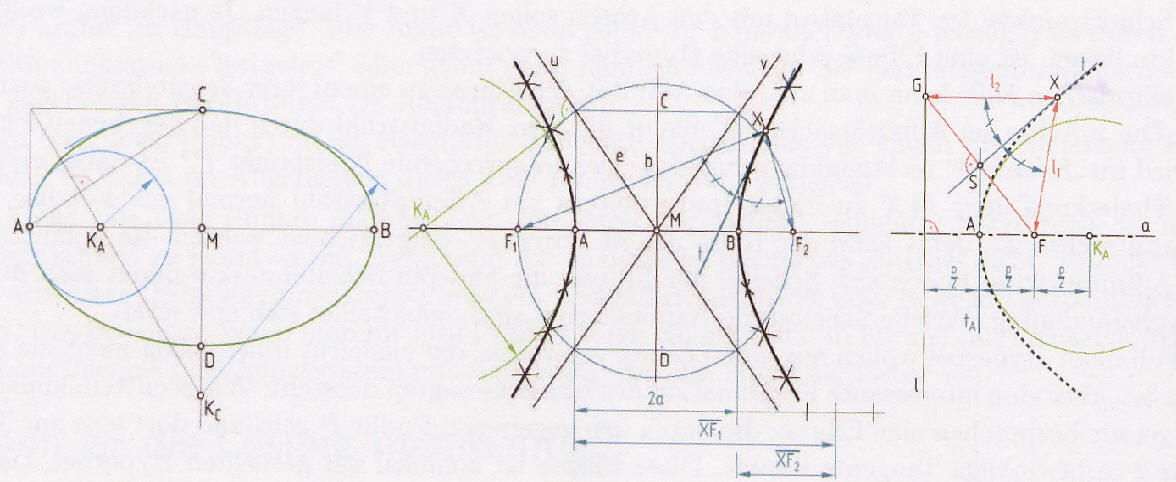
Übungsaufgaben zur Ellipse (58 bzw. 60 an der Zahl) sowie
ein Nachschlag
(So gut wie) alle Übungsaufgaben zu den Kegelschnitten
lassen eine Selbstkontrolle zu, weshalb
sich die Bekanntgabe von Lösungen erübrigt und daher lediglich in speziellen
Einzelfällen via
e-m@il erfolgen
wird!
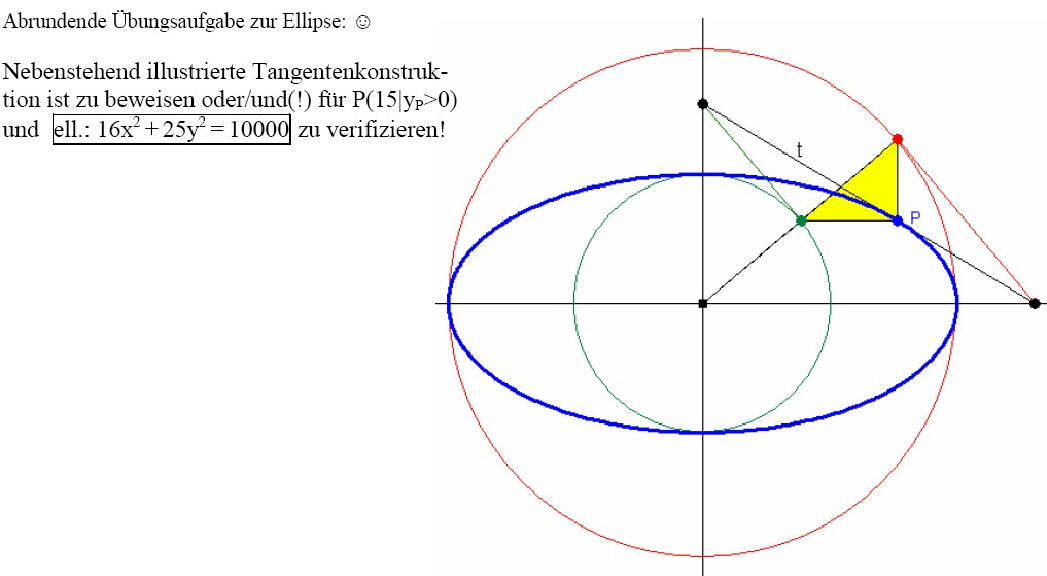
Ebenso abrundende Aufgabe zur Parabel (auch als
pdf-file für zwei, also
gleich für eine/n gute/n Freundin mitausdrucken!☺):
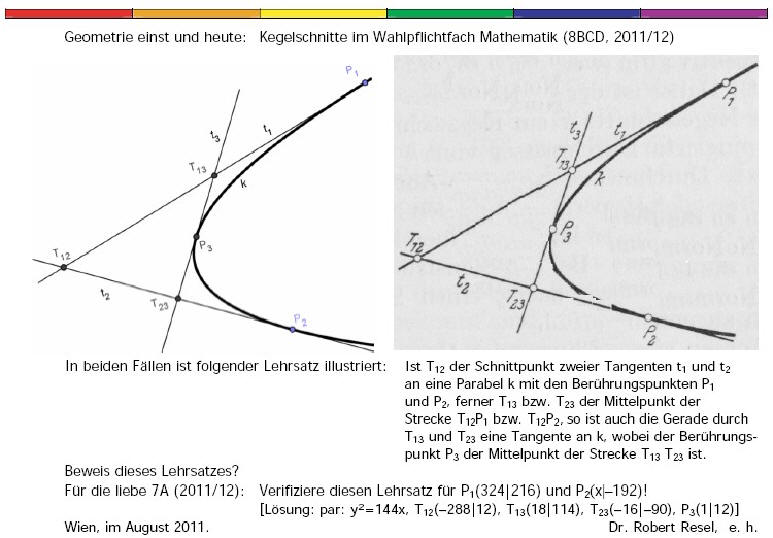
... noch eine vorletzte Anregung zur Beschäftigung mit der
Parabel (sei es aus Interesse, zwecks Übung or whatever):
Lege auf den Brennstrahl b eines beliebigen Parabelpunkts P
die Normale n durch P, der zweite ge-
meinsame Punkt heiße Q, der Schnittpunkt der Tangenten tP
und tQ sei mit R bezeichnet. Dann gilt:
R kann nie auf der Leitgerade der Parabel liegen.
V E R I F I Z I E R E D I E S E N S
A T Z A N E I N E M S E L B S T G E W Ä H L
T E N B E I S P I E L O D E R / U N D B E W
E I S E I H N ! ! !
Schließlich noch eine allerletzte Übungsmöglichkeit zur
analytischen Geometrie der Parabel:
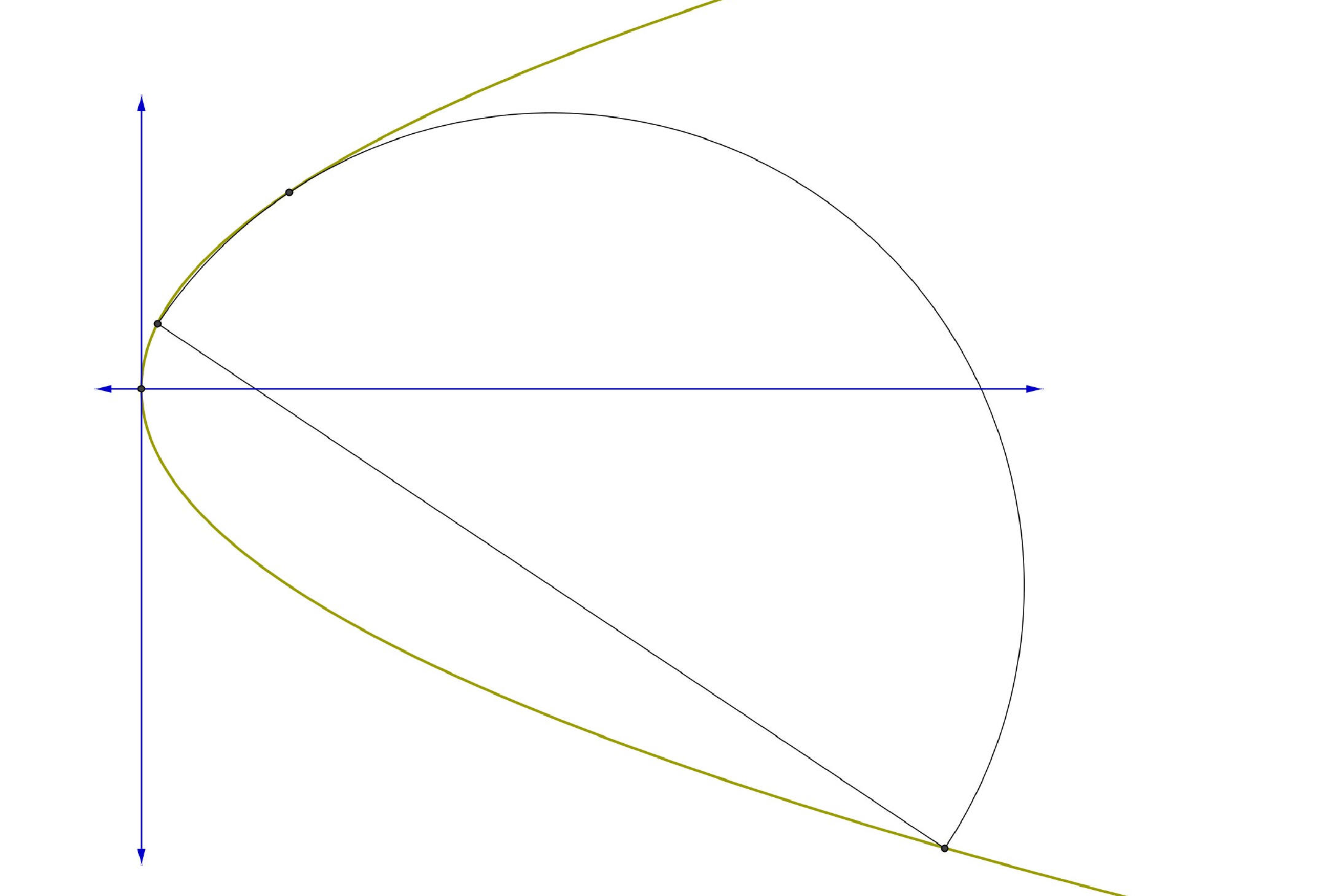
Liegen zwei Punkte A und B auf einer Parabel par in erster
Hauptlage mit dem Parameter p
derart, dass sich ihre y-Koordinaten um exakt 4p unterscheiden, so geht durch A,
B sowie
jenen Punkt C auf par, für den yA+yB+2yC=0
gilt, ein Kreis k, der par in A und B schneidet
und in C berührt. Ferner ist die Parabelsehne AB ein Durchmesser dieses Kreises.
Verifiziere
diesen schönen Lehrsatz der Elementargeometrie am Beispiel des Punkts A(9/12),
wobei B
im vierten Quadranten liegen soll! (Die rechte Abbildung illustriert diesen
Sachverhalt, aber
nicht für das vorliegende Beispiel!)